10 Facts From The Bizarre World Of Infinite Math

In the late 19th century, German mathematician Georg Cantor discovered “transfinite” mathematics, or mathematics beyond infinity. With this early work, we were introduced to a world where there are numbers larger than infinity and equations that do not follow common sense rules of arithmetic. Suffice to say, it’s probably not the stuff you learned in high school.

Cantor’s work was initially controversial and was vitriolically attacked by some of the most important mathematical figures of his day. However, it gradually came to be accepted as canon and has helped pave the way for set theory, which itself is a potential undergirding for all of mathematics.

10 Infinity Plus One (Or Two, Or Infinity) Equals Infinity

It turns out that this old childhood adage has something to it. Given the nature of infinity, any number added to, subtracted from, multiplied by, or divided by it equals infinity. This is seen in a classic infinity puzzle known as Hilbert’s hotel paradox:

There is a hotel that has an infinite number of rooms. A weary traveler arrives and requests a room but is informed that all of the rooms are occupied. How can the hotel not have any more rooms, since it has infinite rooms? What should the traveler do?

The answer is that the traveler should request that the person in room one should move to room two, the person in room two should move to room three, and so forth . . . and she takes room one. Infinity is infinitely elastic and can be expanded or shrunk in any way to fit whatever it needs to, whether it’s one traveler or a googolplex (yes, that’s an actual number) travelers.^[1]

9 There Are As Many Odd Numbers (And As Many Numbers That End In 123 or 423) As There Are Numbers

Infinity is so malleable because, like Hilbert’s hotel, any series of infinite numbers can be put into what is termed a “one-to-one correspondence” with any infinite part of that series. In layperson’s terms, that means that if you take all positive whole numbers (0, 1, 2, 3, 4 . . . ) and all positive even numbers (0, 2, 4, 6, 8 . . . ), each of the whole numbers can be matched up with an even number. So zero can be matched up with zero, one can be matched up with two, two can be matched up with four, and so forth.

Since the two series (or “sets”) of numbers match up for each number, we are justified in saying that they are the same size. Called the Galileo paradox after its famous discoverer, this thought experiment shows that the size of infinity cannot be changed using the crude tools of basic arithmetic like division or the addition of finite numbers. For that, you need something more sophisticated.^[2]

8 Some Infinities Are Bigger Than Others

The flip side of the one-to-one correspondence is that if there is an infinite series of numbers that still has numbers left over after being matched up with another infinite series, then we can say that the former series of infinities is actually larger than the infinity that it was matched with. This might seem impossible, but you can probably intuitively grasp a case where this is true: the infinite number of whole numbers (0, 1, 2, 3 . . . ) is smaller than the infinite number of irrational numbers. If you recall from high school math, irrational numbers are numbers like pi that have a series of decimals that go on forever (3.1415 . . . ). Cantor showed that the infinite number of irrational numbers is larger than the infinite number of whole numbers using an ingenious but simple (relative to most groundbreaking mathematical proofs) trick.^[3]

He began by assuming that irrational numbers could be matched up with whole numbers and wrote down a series of numbers between zero and one. (Okay, these are my own random numbers from mashing the keyboard, but you get the point.) There are an infinite number of these rows:

0.1435 . . . matched with 0
0.7683 . . . matched with 1
0.1982 . . . matched with 2
0.9837 . . . matched with 3

And so on. You can then create a number from this series by taking the first digit in the first line, the second digit in the second line, and so on; for the numbers above, this would be 0.1687 . . .

Now, there might be a number of 0.1687 . . . somewhere in this stack of numbers. However, if you add one to each of the digits, then the number becomes 0.2798 . . . , and this number cannot be in the stack, since it is by definition different from any of the numbers in the stack by at least one digit. Therefore, there are still irrational numbers left over after trying to match them up with normal whole numbers. Therefore, we can say that the infinite number of irrational numbers is larger than the infinite number of whole numbers.

If you think that is crazy, hold onto your hat . . .

7 There Are Infinitely Many Levels Of Infinities

Cantor also showed that, just as the number of infinite whole numbers is on a whole different level of infinity than the number of irrational numbers, there is also a type of infinity that is larger than the number of irrational numbers, a level of infinity above that, another one above that, and so on, up through (you guessed it) infinity. Furthermore, any level of infinity added to a higher level of infinity automatically sums to the higher level of infinity in the same way that infinity plus one equals infinity.^[4]

The Reader’s Digest version of why this is the case is that you can take an infinite series of numbers ( for example, 0, 1, 2, 3 . . . ) and then make a larger infinite series by taking the number of all of the different possible combinations of the numbers in the original series. In math, this is called a power set. So for the whole numbers, the power set would include not just 1, 2, 3 . . . but also every combination of numbers in that infinite series of numbers including 1 billion and 1, 2, 13, 2 million . . . etc. Once you’ve made your first power set, there is no reason why you cannot make a power set of the power set, or a power set of a power set of a power set of a power set . . . 

6 All Of This Eventually Drove Georg Cantor Insane

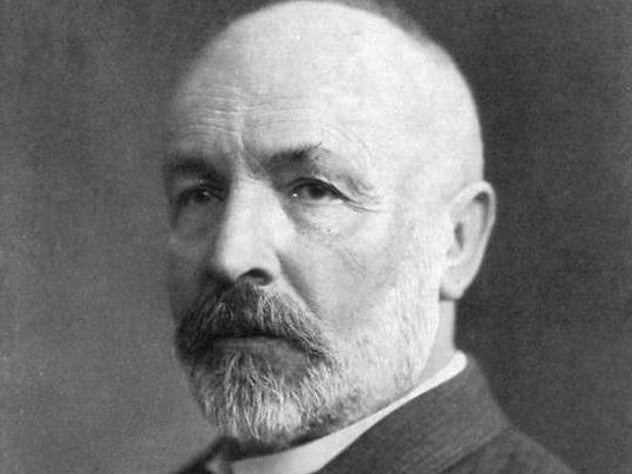
As you can imagine, dwelling on all of this too much can do a number on your sense of reality, and that is exactly what happened to its discoverer. Cantor believed that the “next” level of infinity after the whole numbers was the number of irrational numbers; the only problem was that he could not prove it.

This famous mathematical problem, labeled the continuum hypothesis (he eventually just started saying that God revealed to him that the continuum hypothesis was true), combined with the vicious attacks upon his work, eventually led to a psychological collapse, and he spent the rest of his days in and out of hospitals while trying to prove that Francis Bacon wrote Shakespeare’s plays.^[5]

5 The Problem That Drove Cantor Insane Is Unsolvable

Some people have tried to provide a rigorous foundation for math by using a series of axioms, or statements that are supposedly so commonsensical that they can be trusted without any prior explanation. (E.g. One cannot equal two. Why? Because!)

In the 1960s, mathematician Paul Cohen proved that the continuum hypothesis is unsolvable if we assume that the most commonly used axioms are true. However, to this day, mathematical work continues to be done under the assumption that the axioms are true and that the continuum hypothesis is false, as well as the reverse assumption that the conventional axioms are true as well as the continuum hypothesis. Mathematicians consider the different assumptions about the continuum hypothesis as belonging to different “mathematical universes,” since we cannot prove that one or the other is true.^[6]

4 The Symbol For Infinity That Cantor Chose Is A Hebrew Letter

Like astronomers and biologists, mathematicians who discover some new concept or important value get to have at least some input into what its name will be. Given that kind of power, you would think there would be more Klingon characters in high-level math today, but no. As creative as mathematicians are, hardly any of them want to stray from the very conventional Greek symbols, which is why different Greek letters can mean so many different things depending on which branch of math you are using—we simply have so many more mathematical constants and concepts than Greek letters.

While his religious background is still debated by historians, Cantor saw what he was doing as a way to approach the divine through mathematics, so he decided that the different levels of infinity would be symbolized by the first letter in the Hebrew alphabet: aleph. The set of all whole numbers would be aleph-naught, or aleph with a zero subscript. The next highest infinity would be aleph-one, which, as we have mentioned, may or may not be the number of irrational numbers.^[7]

3 There Is A Level Of Infinity In Which Infinity Plus One Does Not Equal One Plus Infinity

In addition to the aleph numbers, Cantor also came up with omega numbers. The first omega number is defined as the smallest number that is larger than the number of whole numbers, or the first number after aleph-naught. To draw on Hilbert’s hotel example again, if the number of rooms is aleph-naught, then the first omega number is a shack outside the hotel. The next omega number after that is simply omega plus one. What this means, however, is that one plus omega is different than omega plus one, since the one in the former would be simply absorbed by omega (since infinity is malleable), whereas the one after omega represents the next step.^[8]

Unfortunately, understanding more technical proof of this supersedes the abilities of your humble author’s intellect, but I read it in a book, so it has to be true.

2 Infinity Minus Infinity Does Not Equal Zero

Infinity minus infinity is undefined in the same way that dividing by zero is undefined.

To give an example of why this is, since infinity plus one equals infinity ([infinity + 1] = [infinity]), if we subtract infinity from both sides, we are left with 1 = 0. Similarly, and for many of the same reasons, infinity divided by infinity is not one but is also undefined.^[9]

1 This Actually Has Real-World Scientific Applications

Like many other areas in mathematics, what started as a purely theoretical thought experiment has been found to have implications in the hard sciences. For example, some quantum mechanics equations sum to infinity; in practice, physicists tweak the equation to make calculations doable, but it is not clear if doing so is justified, given what we know about transfinite math.

In cosmology, whether the universe is infinitely large, space is infinitely divisible, the universe will expand forever, or whether there are infinite universes are all open questions that draw on infinite logic.^[10] Some researchers have even found applications of Hilbert’s hotel paradox in both quantum and classical optics.

Stephen Cranney is a postdoctoral researcher in sociology and demography at Baylor University, specializing in fertility, religion, and sexuality. He has only recently recovered from his US public school exposure to math and now appreciates math as the art form that it is.