 Movies and TV
Movies and TV  Movies and TV
Movies and TV  History
History 10 Things You Never Knew About Presidential First Ladies
 Movies and TV
Movies and TV 10 Zombie Movies That Will Actually Terrify You
 Humans
Humans 10 Times Scientists Were Absolutely Sure… and Absolutely Wrong
 Our World
Our World 10 Pivotal Moments for Life on Earth
 Movies and TV
Movies and TV 10 Most Realistic Medical TV Shows of All Time
 Creepy
Creepy 10 Eerie & Mysterious Ghosts of the Pacific Coast
 Weird Stuff
Weird Stuff 10 Typos That Accidentally Changed History
 History
History 10 Times Trickery Won Battles
 Technology
Technology 10 Awesome Upgrades to Common Household Items
 Movies and TV
Movies and TV 10 Movie Flops That Found Their Way to Cult Classic Status
 History
History 10 Things You Never Knew About Presidential First Ladies
 Movies and TV
Movies and TV 10 Zombie Movies That Will Actually Terrify You
Who's Behind Listverse?

Jamie Frater
Head Editor
Jamie founded Listverse due to an insatiable desire to share fascinating, obscure, and bizarre facts. He has been a guest speaker on numerous national radio and television stations and is a five time published author.
More About Us Humans
Humans 10 Times Scientists Were Absolutely Sure… and Absolutely Wrong
 Our World
Our World 10 Pivotal Moments for Life on Earth
 Movies and TV
Movies and TV 10 Most Realistic Medical TV Shows of All Time
 Creepy
Creepy 10 Eerie & Mysterious Ghosts of the Pacific Coast
 Weird Stuff
Weird Stuff 10 Typos That Accidentally Changed History
 History
History 10 Times Trickery Won Battles
 Technology
Technology 10 Awesome Upgrades to Common Household Items
10 Coolest Mathematics Results
Many people are put off by the obscure symbols and strict rules of math, giving up on a problem as soon as they see both numbers and letters involved. But while math may be dense and difficult at times, the results it can prove are sometimes beautiful, mind-boggling, or just plain unexpected. Results like:
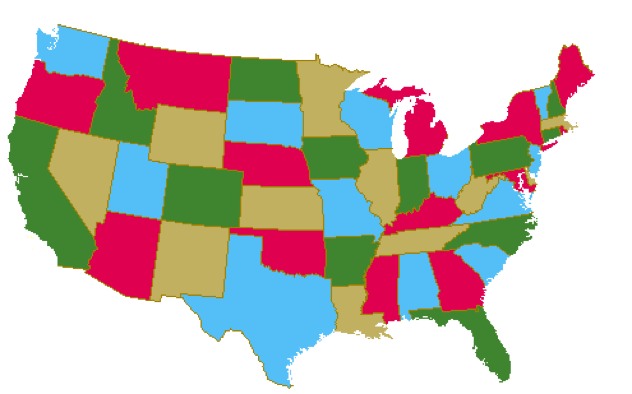
The 4-Color Theorem was first discovered in 1852 by a man named Francis Guthrie, who at the time was trying to color in a map of all the counties of England (this was before the internet was invented, there wasn’t a lot to do). He discovered something interesting—he only needed a maximum of four colors to ensure that no counties that shared a border were colored the same. Guthrie wondered whether or not this was true of any map, and the question became a mathematical curiosity that went unsolved for years.
In 1976 (over a century later), this problem was finally solved by Kenneth Appel and Wolfgang Haken. The proof they found was quite complex and relied in part on a computer, but it states that in any political map (say of the States) only four colors are needed to color each individual State so that no States of the same color are ever in contact.

This theorem comes from a branch of math known as Topology, and was discovered by Luitzen Brouwer. While its technical expression is quite abstract, it has many fascinating real world implications. Let’s say we have a picture (for example, the Mona Lisa) and we take a copy of it. We can then do whatever we want to this copy—make it bigger, make it smaller, rotate it, crumple it up, anything. Brouwer’s Fixed Point Theorem says that if we put this copy overtop of our original picture, there has to be at least one point on the copy that is exactly overtop the same point on the original. It could be part of Mona’s eye, ear, or possible smile, but it has to exist.
This also works in three dimensions: imagine we have a glass of water, and we take a spoon and stir it up as much as we want. By Brouwer’s theorem, there will be at least one water molecule that is in the exact same place as it was before we started stirring.

At the turn of the 20th century, a lot people were entranced by a new branch of math called Set Theory (which we’ll cover a bit later in this list). Basically, a set is a collection of objects. The thinking of the time was that anything could be turned into a set: The set of all types of fruit and the set of all US Presidents were both completely valid. Additionally, and this is important, sets can contain other sets (like the set of all sets in the preceding sentence). In 1901 famous mathematician Bertrand Russell made quite a splash when he realized that this way of thinking had a fatal flaw: namely, not anything can be made into a set.
Russell decided to get meta about things and described a set that contained all those sets which do not contain themselves. The set of all fruit doesn’t contain itself (the jury’s still out on whether it contains tomatoes), so it can be included in Russell’s set, along with many others. But what about Russell’s set itself? It doesn’t contain itself, so surely it should be included as well. But wait…now it DOES contain itself, so naturally we have to take it out. But we now we have to put it back…and so on. This logical paradox caused a complete reformation of Set Theory, one of the most important branches of math today.

Remember Pythagoras’ theorem from school? It has to do with right-angled triangles, and says that the sum of the squares of the two shortest sides are equal to the square of the longest side (x squared + y squared = z squared). Pierre de Fermat’s most famous theorem is that this same equation is not true if you replace the squared with any number greater than 2 (you could not say x cubed +y cubed = z cubed, for example), as long as x, y, and z are positive whole numbers.
As Fermat himself wrote: “I have discovered a truly marvelous proof of this, which this margin is too narrow to contain.” That’s really too bad, because while Fermat posed this problem in 1637, it went unproven for quite a while. And by a while, I mean it was proven in 1995 (358 years later) by a man named Andrew Wiles.

It’s a fair assumption that most of the readers of this article are human beings. Being humans, this entry will be particularly sobering: math can be used to determine when our species will die out. Using probability, anyways.
The argument (which has been around for about 30 years and has been discovered and rediscovered a few times) basically says that humanity’s time is almost up. One version of the argument (attributed to astrophysicist J. Richard Gott) is surprisingly simple: If one considers the complete lifetime of the human species to be a timeline from birth to death, then we can determine where on that timeline we are now.
Since right now is just a random point in our existence as a species, then we can say with 95% accuracy that we are within the middle 95% of the timeline, somewhere. If we say that right now we are exactly 2.5% into human existence, we get the longest life expectancy. If we say we are 97.5% into human existence, that gives us the shortest life expectancy. This allows us to get a range of the expected lifespan of the human race. According to Gott, there’s a 95% chance that human beings will die out sometime between 5100 years and 7.8 million years from now. So there you go, humanity—better get on that bucket list.
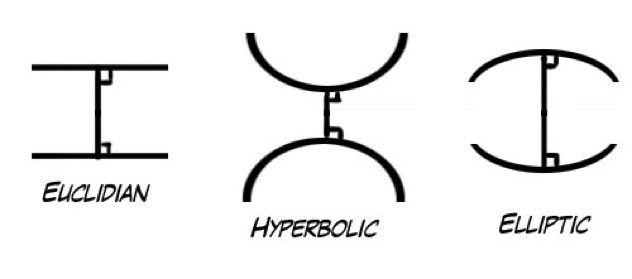
Another bit of math you may remember from school is geometry, which is the part of math where doodling in your notes was the point. The geometry most of us are familiar with is called Euclidean geometry, and it’s based on five rather simple self-evident truths, or axioms. It’s the regular geometry of lines and points that we can draw on a blackboard, and for a long time it was considered the only way geometry could work.
The problem, however, is that the self-evident truths that Euclid outlined over 2000 years ago weren’t so self-evident to everyone. There was one axiom (known as the parallel postulate) that never sat right with mathematicians, and for centuries many people tried to reconcile it with the other axioms. At the beginning of the 18th century a bold new approach was tried: the fifth axiom was simply changed to something else. Instead of destroying the whole system of geometry, a new one was discovered which is now called hyperbolic (or Bolyai-Lobachevskian) geometry. This caused a complete paradigm shift in the scientific community, and opened the gates for many different types of non-Euclidean geometry. One of the more prominent types is called Riemannian geometry, which is used to describe none other than Einstein’s Theory of Relativity (our universe, interestingly enough, doesn’t abide by Euclidean geometry!).
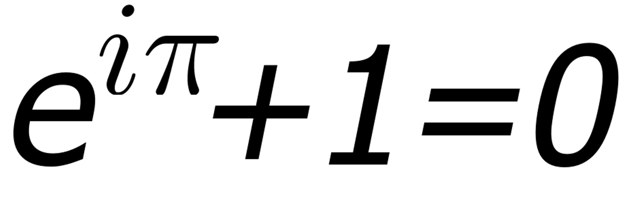
Euler’s Formula is one of the most powerful results on this list, and it’s due to one of the most prolific mathematicians that ever lived, Leonhard Euler. He published over 800 papers throughout his life—many of them while blind.
His result looks quite simple at first glance: e^(i*pi)+1=0. For those that don’t know, both e and pi are mathematical constants which come up in all sorts of unexpected places, and i stands for the imaginary unit, a number which is equal to the square root of -1. The remarkable thing about Euler’s Formula is how it manages to combine five of the most important numbers in all of math (e, i, pi, 0, and 1) into such an elegant equation. It has been called by physicist Richard Feynman “the most remarkable formula in mathematics”, and its importance lies in its ability to unify multiple aspects of math.

We live in a world that’s dominated by computers. You’re reading this list on a computer right now! It goes without saying that computers are one of the most important inventions of the 20th century, but it might surprise you to know that computers at their core begin in the realm of theoretical mathematics.
Mathematician (and also WW2 code-breaker) Alan Turing developed a theoretical object called a Turing Machine. A Turing Machine is like a very basic computer: it uses an infinite string of tape and 3 symbols (say 0, 1, and blank), and then operates given a set of instructions. Instructions could be to change a 0 to a 1 and move a space to the left, or to fill in a blank and move a space to the right (for example). In this way a Turing Machine could be used to perform any well-defined function.
Turing then went on to describe a Universal Turning Machine, which is a Turing Machine that can imitate any Turing Machine with any input. This is essentially the concept of a stored-program computer. Using nothing but math and logic, Turing created the field of computing science years before the technology was even possible to engineer a real computer.

Infinity is already a pretty difficult concept to grasp. Humans weren’t made to comprehend the never-ending, and for that reason Infinity has always been treated with caution by mathematicians. It wasn’t until the latter half of the 19th century that Georg Cantor developed the branch of math known as Set Theory (remember Russell’s paradox?), a theory which allowed him to ponder the true nature of Infinity. And what he found was truly mind-boggling.
As it turns out, whenever we imagine infinity, there’s always a different type of infinity that’s bigger than that. The lowest level of infinity is the amount of whole numbers (1,2,3…), and it’s a countable infinity. With some very elegant reasoning, Cantor determined that there’s another level of infinity after that, the infinity of all Real Numbers (1, 1.001, 4.1516…basically any number you can think of). That type of infinity is uncountable, meaning that even if you had all the time in the universe you could never list off all the Real Numbers in order without missing some. But wait—as it turns out, there’s even more levels of uncountable infinity after that. How many? An infinite number, of course.

In 1931, Austrian mathematician Kurt Gödel proved two theorems which shook the math world to its very core, because together they showed something quite disheartening: math is not, and never will be, complete.
Without getting into the technical details, Gödel showed that in any formal system (such as a system of the natural numbers), there are certain true statements about the system which cannot be proven by the system itself. Fundamentally, he showed that it is impossible for an axiomatic system to be completely self-contained, which went against all previous mathematical assumptions. There will never be a closed system that contains all of mathematics—only systems that get bigger and bigger as we unsuccessfully try to make them complete.
Michael Alba likes to make stupid jokes on twitter @MichaelPaulAlba. If you follow him, he’ll buy you an imaginary ice cream cone (imaginary chocolate or imaginary vanilla only).





