 Weird Stuff
Weird Stuff  Weird Stuff
Weird Stuff  Movies and TV
Movies and TV 10 Actors Who Almost Didn’t Take Career-Defining Roles
 Technology
Technology 10 Little-Known Shifts in Computer Science
 Religion
Religion 10 Catholic Histories That Reveal Acceptance of Abortion and Contraception
 Politics
Politics 10 Lesser-Known “First and Only” Facts about U.S. Presidents
 Miscellaneous
Miscellaneous 10 Things You May Not Know about the Fourth of July
 History
History 10 Shocking and Gruesome Founding Father Facts They Don’t Teach in School
 Crime
Crime The Ten Most Vicious Los Angeles Killers
 Miscellaneous
Miscellaneous 10 Indispensable Corporations the World Cannot Afford to Lose
 Animals
Animals 10 Unusual Wolves That Made The News
 Weird Stuff
Weird Stuff Ten Unexpected Discoveries Involving Vomit
 Movies and TV
Movies and TV 10 Actors Who Almost Didn’t Take Career-Defining Roles
 Technology
Technology 10 Little-Known Shifts in Computer Science
Who's Behind Listverse?

Jamie Frater
Head Editor
Jamie founded Listverse due to an insatiable desire to share fascinating, obscure, and bizarre facts. He has been a guest speaker on numerous national radio and television stations and is a five time published author.
More About Us Religion
Religion 10 Catholic Histories That Reveal Acceptance of Abortion and Contraception
 Politics
Politics 10 Lesser-Known “First and Only” Facts about U.S. Presidents
 Miscellaneous
Miscellaneous 10 Things You May Not Know about the Fourth of July
 History
History 10 Shocking and Gruesome Founding Father Facts They Don’t Teach in School
 Crime
Crime The Ten Most Vicious Los Angeles Killers
 Miscellaneous
Miscellaneous 10 Indispensable Corporations the World Cannot Afford to Lose
 Animals
Animals 10 Unusual Wolves That Made The News
Top 10 Fascinating Facts About The Number Pi
The most well-known fact about pi—normally rounded to 3.14159—is that it represents the ratio of the circumference of a circle to its diameter. Pi is also an irrational number, so it is incapable of being written as a simple fraction. Therefore, pi is an infinitely long, non-repeating decimal, making it one of the most interesting and mysterious numbers known to man.
10First Calculation

The first calculation of pi is believed to have been obtained by Archimedes of Syracuse around 220 BC. Archimedes derived the formula A = pi r2 by approximating the area of a circle based on the area of a regular polygon inscribed within the circle, and the area of a polygon within which the circle was circumscribed. The two polygons therefore provided the upper and lower bounds for the area of a circle—allowing Archimedes to approximate that the missing piece of the puzzle (pi) lay somewhere between 3 1/7 and 3 10/71.
The prominent Chinese mathematician and astronomer Zu Chongzi (429–501) later calculated pi to be 355/113, although exactly how he was able to reach this incredibly precise measurement remains a mystery, since there are no records of his work.
9A Circle’s True Area Is Unknowable
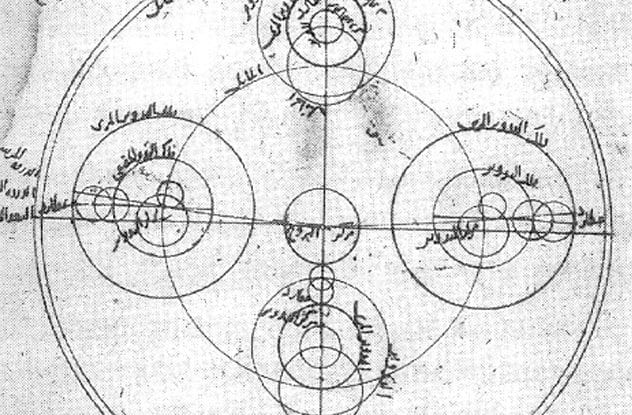
Johann Heinrich Lambert in the 18th century, proved that pi is irrational—it cannot be expressed as an integer-based fraction. Rational numbers can always be written as a fraction, in which both the numerator and the denominator are whole numbers. Although it might be tempting to view pi as a simple ratio of circumference/diameter (pi=C/D), it will always be the case that if the diameter is an integer, the circumference is not an integer, and vice versa.
The irrationality of pi means we can never truly know the circumference (and subsequently the area) of a circle. This frustrating yet seemingly unavoidable fact has led some mathematicians to insist that it is more accurate to think of a circle as having an infinite number of tiny corners, instead of thinking of a circle as being “smooth.”
8Buffon’s Needle
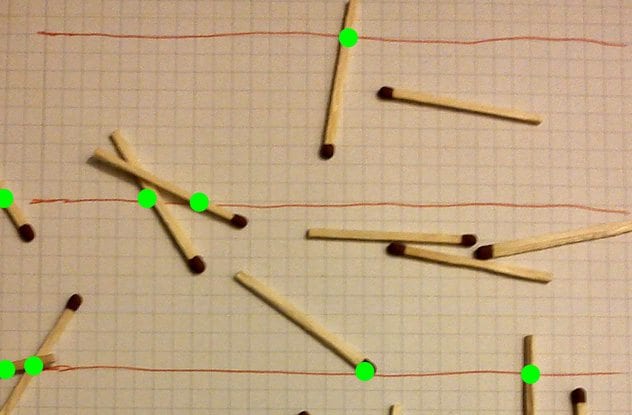
First brought to the attention of geometricians and mathematicians in 1777, Buffon’s needle is one of the oldest and most intriguing problems in the field of geometrical probability. Here’s how it works.
If you were to drop a needle of one unit length onto a sheet of paper with lines separated by the same single unit length, the probability that the needle crosses one of the lines on the page is directly related to the value of pi.
There are two variables involved in the needle drop: 1) the angle at which the needle falls, and 2) the distance from the center of the needle to the closest line. The angle can vary from 0 to 180 degrees and is measured against a line parallel to the lines on the paper.
It turns out the probability that the needle lands so that it cuts a line is exactly 2/pi, or roughly 64 percent. This means that pi could be theoretically calculated using this technique if one had enough patience to sit through enough trials, even though the experiment seems to have nothing to do with circles, or even rounded edges for that matter.
This may be a bit difficult to envision, so experiment with the phenomenon yourself here.
7Pi And The Ribbon Problem

Imagine you take a ribbon and wrap it around the Earth. (Let’s assume for the sake of simplicity that the Earth is a perfect sphere with a circumference of 24,900 miles.) Now, try to determine the needed length of a ribbon that could surround the Earth at a distance of one inch above its surface. If you instinctively believe the second ribbon would need to be significantly longer than the first, you would not be alone. You would, however, be wrong. In fact, the second ribbon would increase in length only by 2pi, or roughly 6.28 inches.
Here’s how this head-scratcher breaks down: Again, assuming that the Earth is a perfect sphere, it can be thought of as a giant circle with a circumference of 24,900 miles at the equator. This means the radius would be 24,900/2pi, or roughly 3,963 miles. Now, the added second ribbon hovering an inch above the Earth’s surface would have a radius one inch longer than that of the Earth’s, leading to the equation C = 2 Pi(r+1), which is equivalent to C = 2 Pi(r) + 2 Pi. From this, we can tell that the circumference of the second ribbon will increase by 2pi. In fact, no matter what the original radius is (whether it is the Earth’s or a basketball’s), increasing a radius by one inch will always lead to an increase of 2pi (just 6.28 inches) in circumference.
6Navigation

Pi plays a prominent role in navigation, especially when it comes to large-scale global positioning. Since humans are quite small compared to the Earth, we tend to think of travel as being linear. However, when planes fly, they are of course flying on an arc of a circle. The flight path therefore must be calculated as such to accurately gauge travel time, fuel use, etc. Additionally, when you locate yourself on Earth using a GPS device, pi must play an important role in these calculations.
So what about navigation that requires even more exact precision over even greater distances than a flight from New York to Tokyo? Susan Gomez, manager of the International Space Station Guidance Navigation and Control (GNC) subsystem for NASA, reveals that most of the calculations NASA runs involving pi use 15 or 16 digits, especially when super-precise calculations are required for the Space Integrated Global Positioning System/Inertial Navigation System (SIGI)—the program that controls and stabilizes spacecraft during missions.
5Signal Processing And Fourier Transform

While pi is best known for making geometric measurements such as calculating the area of a circle, it also plays a prominent role in signal processing, mainly through an operation known as the Fourier transform, which converts a signal to a frequency spectrum. The Fourier transform is called the “frequency domain representation” of the original signal, in that it refers to both the frequency domain and the mathematical operation that associates the frequency domain to a function of time.
Humans and technology alike take advantage of this phenomenon whenever a signal is in need of basic conversion, such as when your iPhone receives a message from a cell tower, or when your ear makes a distinction between sounds of differing pitch. Pi, which appears prominently in the Fourier transform formula, plays a fundamental yet somewhat mysterious role in the conversion process, as it lies in the exponent of Euler’s Number (the famed mathematical constant equal to 2.71828 . . . )
This means that every time you make a call on your cell phone or listen to a broadcast signal, you have pi to partially thank.
4Normal Probability Distribution
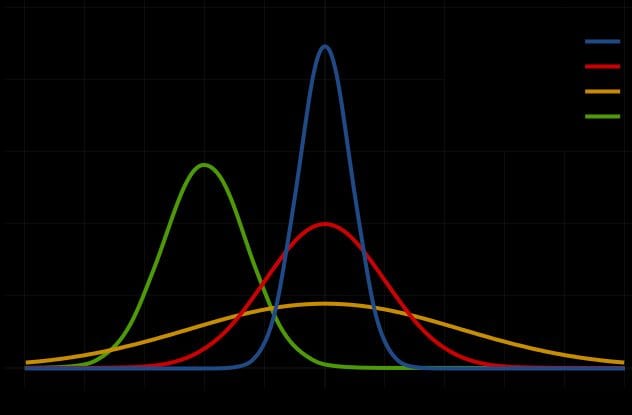
While pi is somewhat expected to be found in operations such as the Fourier transform, which deal primarily with signals (and subsequently waves), it can be surprising to find pi playing a major role in the formula for normal probability distribution. You have doubtless come across this notorious distribution before—it is involved in a wide range of phenomena we see unfold on a regular basis, from dice rolls to test scores.
Whenever you see pi lurking in a complex equation, assume a circle is hidden somewhere within the mathematical fabric. In the case of normal probability distribution, pi is delivered through the Gaussian integral (also known as the Euler–Poisson integral), which features the square root of pi. In fact, all it takes is slight changes in variables in the Gaussian integral to compute the normalizing constant of the normal distribution.
One common yet counterintuitive application of the Gaussian integral involves “white noise,” a normally distributed random variable used to predict everything from wind gusts on a plane to beam vibrations during large-scale construction.
3Meandering Rivers

Pi has a fascinating and unexpected relationship to meandering rivers. A river’s path is mostly described by its sinuosity—its tendency to wind from side to side as it traverses a plain. This can be described mathematically as the length of its winding path divided by the length of the river from its source to its mouth. It turns out that regardless of the river’s length, or how many twists and turns it takes along its path, the average river has a sinuosity of roughly pi.
Albert Einstein made several observations regarding why rivers tend to behave this way. He noticed that water flows faster around the outside of a river bend, leading to faster erosion around the bank, which in turn creates a larger bend. These larger bends meet, causing the river to form a “shortcut” connection. This back-and-forth movement seems to constantly correct itself as the river’s sinuosity moves back toward pi.
2Pi And The Fibonacci Sequence

Throughout most of history, there were only two methods used to compute pi, one invented by Archimedes, and the other by the Scottish mathematician James Gregory.
It turns out, however, that pi can also be calculated using the Fibonacci sequence. Each subsequent number in the Fibonacci sequence is the sum of the previous two numbers. The sequence begins with 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, and continues infinitely. And since the arctangent of 1 is pi/4, this means that pi can be expressed in terms of Fibonacci numbers, by rearranging the equation to be arctan(1)*4=pi.
In addition to being an inherently fascinating and beautiful number set, the Fibonacci sequence plays an important role in a variety of natural occurrences throughout the cosmos. It can model or describe an amazing variety of phenomena, in mathematics and science, art, and nature. The mathematical ideas the Fibonacci sequence leads to—such as the golden ratio, spirals, and curves—have long been appreciated for their beauty, but mathematicians are still struggling to explain the depth of the connection.
1Quantum Mechanics

Pi is undoubtedly an unavoidable and complex staple of our world, but what about the universe at large? Pi manifests itself throughout the universe and is indeed involved in the very equations that seek to explain the nature of the cosmos. In fact, many formulas used in the realm of quantum mechanics, which governs the microscopic world of atoms and nuclei, use pi.
Perhaps the most famous of such equations are the Einstein field equations (also known simply as Einstein’s equations)—a set of 10 equations in Einstein’s general theory of relativity that describe the fundamental interaction of gravitation as a result of space-time being curved by mass and energy. The amount of gravity present in a system is proportional to the amount of energy and momentum, with the constant of proportionality related to G, a numerical constant.








