10 Beautiful Examples of Symmetry In Nature

For centuries, symmetry has remained a subject that’s fascinated philosophers, astronomers, mathematicians, artists, architects, and physicists. The ancient Greeks were downright obsessed with it—and even today we tend to side with symmetry in everything from planning our furniture layout to styling our hair.

No one’s sure why it’s such an ever-present property, or why the mathematics behind it seem to permeate everything around us—but the ten examples below prove that it’s definitely there.

Just be warned: once you’re aware of it, you’ll likely have an uncontrollable urge to look for symmetry in everything you see.

You may have passed by romanesco broccoli in the grocery store and assumed, because of its unusual appearance, that it was some type of genetically modified food. But it’s actually just one of the many instances of fractal symmetry in nature—albeit a striking one.

In geometry, a fractal is a complex pattern where each part of a thing has the same geometric pattern as the whole. So with romanseco broccoli, each floret presents the same logarithmic spiral as the whole head (just miniaturized). Essentially, the entire veggie is one big spiral composed of smaller, cone-like buds that are also mini-spirals.

Incidentally, romanesco is related to both broccoli and cauliflower; although its taste and consistency are more similar to cauliflower. It’s also rich in carotenoids and vitamins C and K, which means that it makes both a healthy and mathematically beautiful addition to our meals.

Not only are bees stellar honey producers—it seems they also have a knack for geometry. For thousands of years, humans have marveled at the perfect hexagonal figures in honeycombs and wondered how bees can instinctively create a shape humans can only reproduce with a ruler and compass. The honeycomb is a case of wallpaper symmetry, where a repeated pattern covers a plane (e.g. a tiled floor or a mosaic).

How and why do bees have a hankering for hexagons? Well, mathematicians believe that it is the perfect shape to allow bees to store the largest possible amount of honey while using the least amount of wax. Other shapes, like circles for instance, would leave a gap between the cells since they don’t fit together exactly.

Other observers, who have less faith in the ingenuity of bees, think the hexagons form by “accident.” In other words, the bees simply make circular cells and the wax naturally collapses into the form of a hexagon. Either way, it’s all a product of nature —and it’s pretty darn impressive.

Sunflowers boast radial symmetry and an interesting type of numerical symmetry known as the Fibonacci sequence. The Fibonacci sequence is 1, 2, 3, 5, 8, 13, 21, 24, 55, 89, 144, and so on (each number is determined by adding the two preceding numbers together).

If we took the time to count the number of seed spirals in a sunflower, we’d find that the amount of spirals adds up to a Fibonacci number. In fact, a great many plants (including romanesco broccoli) produce petals, leaves, and seeds in the Fibonacci sequence, which is why it’s so hard to find a four-leaf clover.

Counting spirals on sunflowers can be difficult, so if you want to test this principle yourself, try counting the spirals on bigger things like pinecones, pineapples, and artichokes.

But why do sunflowers and other plants abide by mathematical rules? Like the hexagonal patterns in a beehive, it’s all a matter of efficiency. For the sake of not getting too technical, suffice it to say that a sunflower can pack in the most seeds if each seed is separated by an angle that’s an irrational number.

As it turns out, the most irrational number is something known as the golden ratio, or Phi, and it just so happens that if we divide any Fibonacci or Lucas number by the preceding number in the sequence we get a number close to Phi (1.618033988749895 . . .) So, for any plant following the Fibonacci sequence, there should be an angle that corresponds to Phi (the “golden angle”) between each seed, leaf, petal, or branch.

In addition to plants, some animals, like the nautilus, exhibit Fibonacci numbers. For instance, the shell of a nautilus is grown in a “Fibonacci spiral.” The spiral occurs because of the shell’s attempt to maintain the same proportional shape as it grows outward. In the case of the nautilus, this growth pattern allows it to maintain the same shape throughout its whole life (unlike humans, whose bodies change proportion as they age).

As is often the case, there are exceptions to the rule—so not every nautilus shell makes a Fibonacci spiral. But they all adhere to some type of logarithmic spiral. And before you start thinking that these cephalopods could have kicked your butt in math class, remember that they’re not consciously aware of how their shells are growing, and are simply benefiting from an evolutionary design that lets the mollusk grow without changing shape.

Most animals have bilateral symmetry—which means that they can be split into two matching halves, if they are evenly divided down a center line. Even humans possess bilateral symmetry, and some scientists believe that a person’s symmetry is the most important factor in whether we find them physically beautiful or not. In other words, if you have a lopsided face, you’d better hope you have a lot of other redeeming qualities.

One animal might be considered to have taken the whole symmetry-to-attract-a-mate thing too far; and that animal is the peacock. Darwin was positively peeved with the bird, and wrote in an 1860 letter that “The sight of a feather in a peacock’s tail, whenever I gaze at it, makes me sick!”

To Darwin, the tail seemed burdensome and didn’t make evolutionary sense since it didn’t fit his “survival of the fittest” theory. He remained furious until he came up with the theory of sexual selection, which asserts that animals develop certain features to increase their chances of mating. Apparently peacocks have the sexual selection thing down pat, since they are sporting a variety of adaptations to attract the ladies, including bright colors, a large size, and symmetry in their body shape and in the repeated patterns of their feathers.

There are around 5,000 types of orb web spiders, and all create nearly perfect circular webs with almost equidistant radial supports coming out of the middle and a spiral woven to catch prey. Scientists aren’t entirely sure why orb spiders are so geometry inclined since tests have shown that orbed webs don’t ensnare food any better than irregularly shaped webs.

Some scientists theorize that the orb webs are built for strength, and the radial symmetry helps to evenly distribute the force of impact when prey hits the web, resulting in less rips in the thread. But the question remains: if it really is a better web design, then why aren’t all spiders utilizing it? Some non-orb spiders seem to have the capacity, and just don’t seem to be bothered.

For instance, a recently discovered spider in Peru constructs the individual pieces of its web in exactly the same size and length (proving its ability to “measure”), but then it just slaps all these evenly sized pieces into a haphazard web with no regularity in shape. Do these Peruvian spiders know something the orb spiders don’t, or have they not discovered the value in symmetry?

Give a couple of hoaxers a board, some string, and the cloak of darkness, and it turns out that people are pretty good at making symmetrical shapes too. In fact, it’s because of crop circles’ incredible symmetries and complexities of design that, even after human crop-circle-makers have come forward and demonstrated their skills, many people still believe only space aliens are capable of such a feat.

It’s possible that there has been a mixture of human and alien-made crop circles on earth—yet one of the biggest hints that they are all man-made is that they’re getting progressively more complicated. It’s counter-intuitive to think that aliens would make their messages more difficult to decipher, when we didn’t even understand the first ones. It’s a bit more likely that people are learning from each other through example, and progressively making their circles more involved.

No matter where they come from, crop circles are cool to look at, mainly because they’re so geometrically impressive. Physicist Richard Taylor did a study on crop circles and discovered—in addition to the fact that about one is created on earth per night—that most designs display a wide variety of symmetry and mathematical patterns, including fractals and Fibonacci spirals.

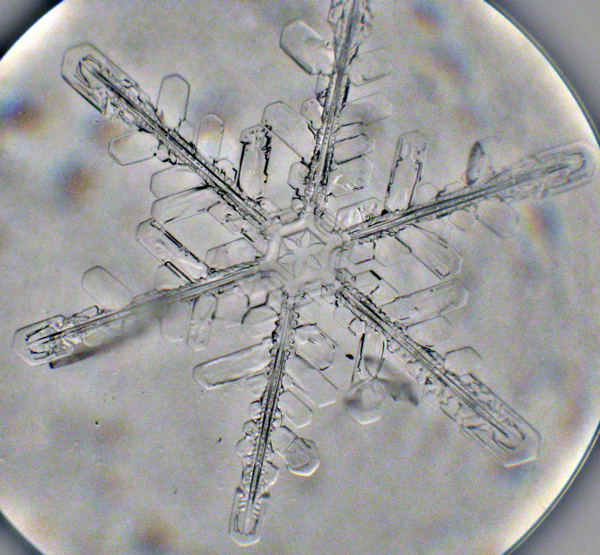
Even something as tiny as a snowflake is governed by the laws of order, as most snowflakes exhibit six-fold radial symmetry with elaborate, identical patterns on each of its arms. Understanding why plants and animals opt for symmetry is hard enough to wrap our brains around, but inanimate objects—how on earth did they figure anything out?

Apparently, it all boils down to chemistry; and specifically, how water molecules arrange themselves as they solidify (crystallize). Water molecules change to a solid state by forming weak hydrogen bonds with each other. These bonds align in an ordered arrangement that maximizes attractive forces and reduces repulsive ones, which happens to form the overall hexagonal shape of the snowflake. But as we’re all aware, no two snowflakes are alike—so how is it that a snowflake is completely symmetrical with itself, while not matching any other snowflake?

Well, as each snowflake makes its descent from the sky it experiences unique atmospheric conditions, like humidity and temperature, which effect how the crystals on the flake “grow.” All the arms of the flake go through the same conditions and consequently crystallize in the same way – each arm an exact copy of the other. No snowflake has the exact same experience coming down and therefore they all look slightly different from one another.

As we’ve seen, symmetry and mathematical patterns exist almost everywhere we look—but are these laws of nature limited to our planet alone? Apparently not. Having recently discovered a new section on the edges of the Milky Way Galaxy, astronomers now believe that the galaxy is a near-perfect mirror image of itself. Based on this new information, scientists are more confident in their theory that the galaxy has only two major arms: the Perseus and the Scutum-Centaurus.

In addition to having mirror symmetry, the Milky Way has another incredible design—similar to nautilus shells and sunflowers—whereby each “arm” of the galaxy represents a logarithmic spiral beginning at the center of the galaxy and expanding outwards.

With the sun having a diameter of 1.4 million kilometers and the Moon having a diameter of a mere 3,474 kilometers, it seems almost impossible that the moon is able to block the sun’s light and give us around five solar eclipses every two years.

How does it happen? Coincidentally, while the sun’s width is about four hundred times larger than that of the moon, the sun is also about four hundred times further away. The symmetry in this ratio makes the sun and the moon appear almost the same size when seen from Earth, and therefore makes it possible for the moon to block the sun when the two are aligned.

Of course, the Earth’s distance from the sun can increase during its orbit—and when an eclipse occurs during this time, we see an annular, or ring, eclipse, because the sun isn’t entirely concealed. But every one to two years, everything is in precise alignment, and we can witness the spectacular event known as a total solar eclipse.

Astronomers aren’t sure how common this symmetry is between other planets, suns, and moons, but they think it’s pretty rare. Even so, we shouldn’t suppose we’re particularly special, since it all seems to be a matter of chance. For instance, every year the moon drifts around four centimeters further away from Earth, which means that billions of years ago, every solar eclipse would have been a total eclipse.

If things keep going the way they are, total eclipses will eventually disappear, and this will even be followed by the disappearance of annular eclipses (if the planet lasts that long). So it appears that we’re simply in the right place at the right time to witness this phenomenon. Or are we? Some theorize that this sun-moon symmetry is the special factor which makes our life on Earth possible.

Content and copy writer by day and list writer by night, S.Grant enjoys exploring the bizarre, unusual, and topics that hide in plain sight. Contact S.Grant at [email protected].